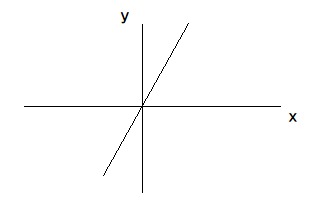2023 年 1 月 27 日更新:
本文正在施工中,将原作业部落的文章迁移到这里。
因为早年撰文不注意,本文中格式存在各种问题(如中英文标点乱用、数学符号不规范、中英文间无空格等等),需要修复完毕后才能继续更新,预计会于最近几天完成。敬请关注。2023 年 2 月 13 日更新:
首次更新完成,修复了大部分格式问题,但仍有少量问题未修复,如有发现请在评论区指出,谢谢。
目前网站可能比较卡顿,考虑一下科学上网吧。
\[\lim_{学习 \to 坚持} 学习=成功\]
前言
非常高兴你能浏览到这篇文章。 我也不太清楚我写作的动机,可能纯属兴趣使然吧。
参考书籍
- 《高等数学(第六版)》上册
同济大学数学系 编
高等教育出版社 出版
- 《7天搞定微积分》
石山平 大上丈彦 著 李巧丽 译
南海出版公司 出版
- 《Principles of Mathematical Analysis》
Walter Rudin 著
McGraw-Hill Education 出版
我是否适合看下去?
在看这篇文章前,你至少需要掌握以下知识:
- 至少初中水平的数学应用能力
- 至少小学水平的阅读能力
- 耐心和对数学的热情
- 以上三条是扯淡
- 这条也是
What’s calculus?
在正式开始学习微积分前,首先我们得明白微积分是啥。
百度一下,我们很容易找到这样的描述:
微积分(Calculus)是高等数学中研究函数的微分、积分以及有关概念和应用的数学分支。它是数学的一个基础学科。 内容主要包括极限、微分学、积分学及其应用。 微分学包括求导数的运算,是一套关于变化率的理论。 它使得函数、速度、加速度和曲线的斜率等均可用一套通用的符号进行讨论。 积分学,包括求积分的运算,为定义和计算面积、体积等提供一套通用的方法。
诶诶诶,别跑啊,我知道这种专家写出来的东西不是一般人能领会得了的。。
简单的说,微积分学是高等数学(并不是高中数学)的重要组成部分,它的地位,相当于小学的四则运算或是初中的方程运算。它非常奇怪、麻烦,可是在高等数学中,你时时刻刻都要用到它。
当然,人们不会故意发明奇怪、麻烦的东西来为难自己,它的应用十分广泛,我们在后面会慢慢提到。
它主要分成两个部分:微分和积分,它们相辅相成,虽各有变化却互为表里,是一对基佬兄弟。我们会在接下来的文章中分别讨论这两个东西。
废话不多说,马上上干货~~
一、导数
导数是微分学的主要内容。翻回去看看百度百科对导数的解释:
导数描述一个函数的变化率。
这是啥么意思呢?变化率是个什么东西?
1.1 First Blood —— 斜率
先来看个函数图像:
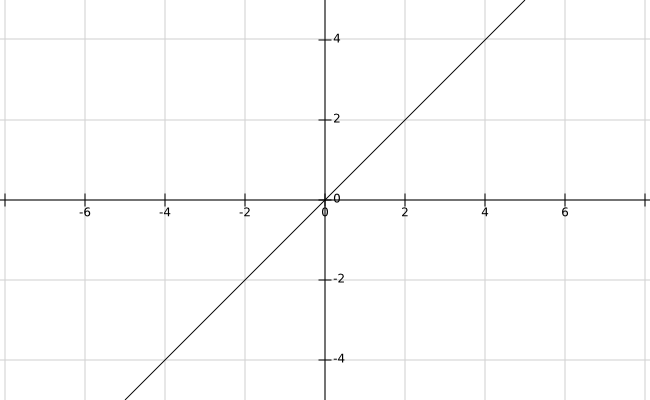
相信你一口就能报出这个函数的解析式:$\(y=x\)$
然后,我们再看个稍微复杂点的图像:
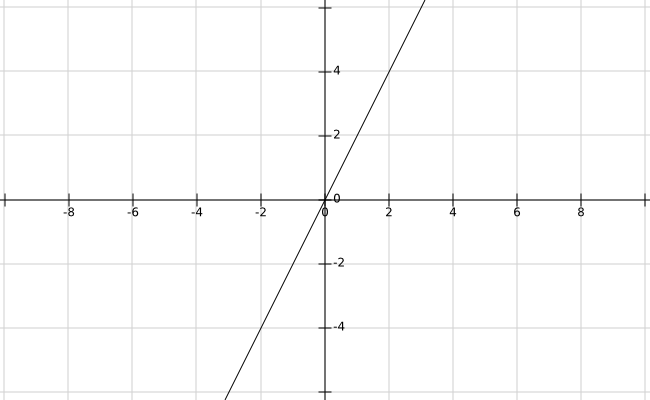
额,这哪里复杂了嘛!明明还是个一次函数啊。。。
不不不,差别大了去了,试试找出这两个函数图像的不同之处?
上下滚动页面,你应当能够看出图像倾斜程度存在着区别,有的数学老师也叫它「\(k\) 决定函数陡平」啥啥的。
回忆一次函数的表达式:$\(y = kx+b (k≠0)\)\( 哈,所以上面这个式子里,**\)k$值的大小就代表着图像倾斜程度的大小**,不是吗?
好了,你的头脑中已经有了基本的微分概念了,同学们,下课!
 哈哈,开个玩笑,还是先别急着关掉页面(从哪里能找到这么没节操的文章 真是)。
哈哈,开个玩笑,还是先别急着关掉页面(从哪里能找到这么没节操的文章 真是)。
不过这句话并没有问题,应当说,从初中学习函数开始,我们就有了对于这些知识的模糊概念,只是它们尚未发掘出来。所以这篇所谓的教程,其实就是帮助万恶的数学老师解决这些概念问题…
还是回到上面这个简单的例子。我们说\(y=x\)与\(y=2x\)这两个函数的倾斜程度不同,因为\(y=2x\)显得更”陡”一些。
虽然小明同学觉得这样描述很好,但是呢,数学家们就是不满足于「a 比 b 陡」这样听起来不是很清楚(也可能是因为他们语文阅读能力不行)的描述方式,(这样听起来不够炫酷狂霸拽)于是发明了一个很好(奇)听(怪)的名字用来描述一条线的陡峭程度,这就是————斜率。
当当!我们终于接触到了第一个数学定义。
呃…虽说这个定义还不完整,甚至你还没弄清啥意思,不过万事总有个开头的,是吧?
接下来我们将慢慢解释斜率这个听起来很高大上的名词。
既然说斜率是个数值,是数值就应该能被写出来。那么我们怎么表示它呢?
再再一次回到上面的例子。容易发现,当\(k=2\)时,图像明显比\(k=1\)时的要陡峭不少。继续画下去:\(k=3、4、5、6、7...\)
图像会越来越陡。
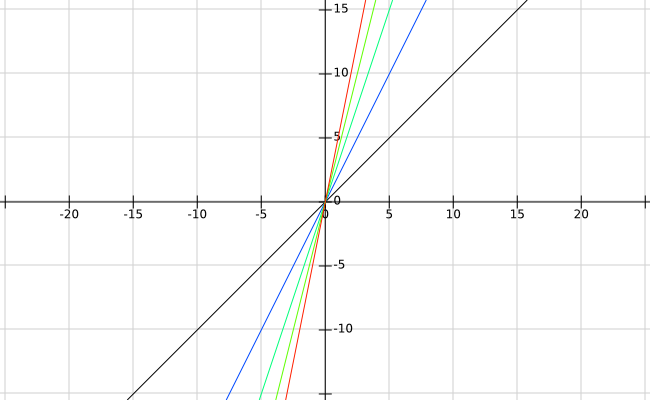 我们发现,\(k\)值增大使得函数更陡峭。
因此,对于一次函数,我们可以用k值大小来表示它的斜率。
我们发现,\(k\)值增大使得函数更陡峭。
因此,对于一次函数,我们可以用k值大小来表示它的斜率。
这个定义听起来很唐突、很随意啊…高大上的感觉顿时都没有了…
更一般地说,斜率也可以这么得出:
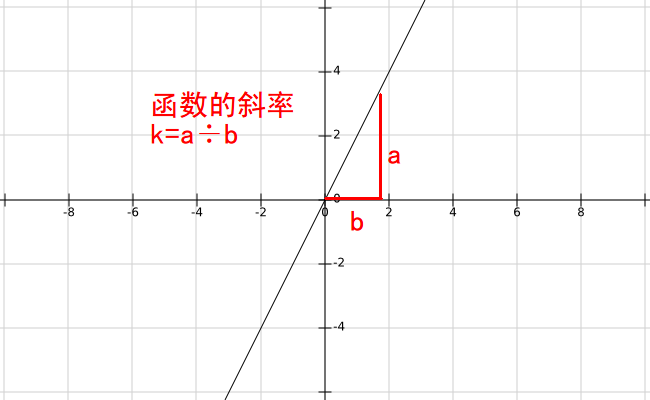
这样,我们对于斜率就有精确的定义了,它不再是一个模糊的概念,而是一个可以拿来比较大小的数值了。比方说,\(y=2x\)的斜率就是\(2\)。
你可能被这些概念搞得有点懵。重新强调一遍,斜率描述一条线的陡峭程度。而一次函数的\(k\)值越大,图像越陡,所以对于一次函数,我们可以用\(k\)值大小来描述它的斜率。
如果你就是没办法把\(k\)和斜率联系起来,稍微喘口气,再往下看吧。
1.1.1 [选读]斜率的严格定义
(对于初三及以上水平的读者,可以有选择性地阅读这些标有「[选读]」文字的部分,因为这些部分可以加深对一些知识的理解。如果你不想看,跳过也没关系。
警告:数学重灾区,请在监护人的陪同下观看。)
先看看百度百科上的斜率词条:
slope,又称「角系数」,是一条直线对于横坐标轴正向夹角的正切,反映直线对水平面的倾斜度。
 如图,\(直线P_1P_2\)的斜率即为\(k=\tan\alpha=\frac{y\_2-y\_1}{x\_2-x\_1}\)。
其中\(α\)又被称为
如图,\(直线P_1P_2\)的斜率即为\(k=\tan\alpha=\frac{y\_2-y\_1}{x\_2-x\_1}\)。
其中\(α\)又被称为倾斜角,取值范围为\(0^\circ \leq \alpha<180^\circ\)。
故:当直线的斜率存在时,斜截式\(y=kx+b\),其斜率即为\(k\)。
1.2 点的斜率?
到现在为止,我们所讨论的函数都仅限于一次函数。你可能觉得数学家们真是一群闲得蛋疼的人,一个简单的\(k\)值都要起个难听的名字。况且,这和微积分有个卵关系?
别猴急,我们先来进一步讨论斜率的含义。在我们搞清楚这些基本概念前,空谈微积分是没啥意义的。
言归正传。 对于二次函数或者反比例函数,又该如何表示它的斜率呢?
先来看看这个熟悉的二次函数吧。
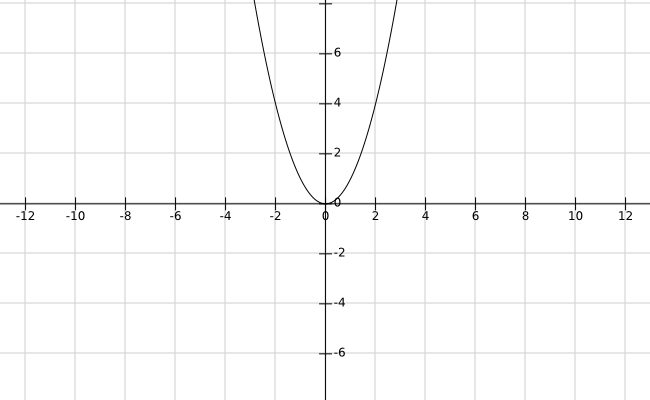 相信这样简单的U型的函数,你已经非常熟悉了。
但是,在表示它的斜率时,你会发现有点小麻烦,不,是大麻烦。
相信这样简单的U型的函数,你已经非常熟悉了。
但是,在表示它的斜率时,你会发现有点小麻烦,不,是大麻烦。
对于这个函数,我们还能用\(k\)值来表示它的倾斜程度吗?
稍做思考,你会发现行不通。这个函数的陡峭程度不是用一个”陡”或者”平”能描述得了的。它的图像自左向右,先是快速下降,再逐渐减缓,在原点处猛地拐了一个180度的大弯,又开始逐渐变快、飞速上升。
那么,显然它的整个图像的斜率已经无法直接表示了。我们是不是能求出其中一段的斜率呢?
比方说,在y轴右边的这半个曲线,如果只看从0到2这一小段,你会觉得它很像\(y=2x\)的一小段。
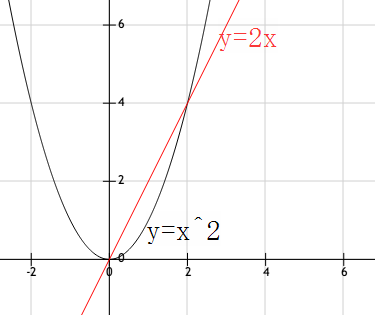
嘿,这一段的斜率是不是差不多是\(2\)呢?
不对。
唔,也不能说是全错,毕竟只是弯了点啊。。
所以让我们继续放大图像,取更小的区间试试?
于是我们放大大大大大大大大大大大大大(此处省略 N 个大)
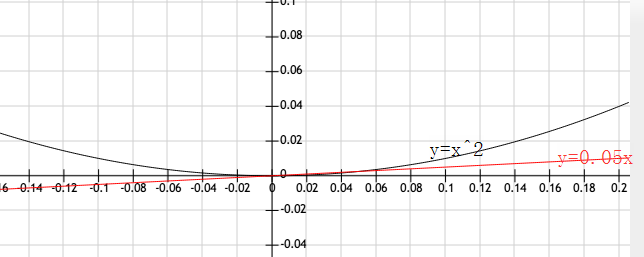
诶,这两个图像看起来有一部分重合了呢?! 也不全然,毕竟前者是曲线,后者是直线呐。。 显然,即使我们放大下去,两个图像也很难有相同的部分,或者说不可能有。 看来硬凑直线的方法行不通,得换个思路。
咳,如果你看得一头雾水,稍微提示一下:
我们是否能对图像上的一个点求斜率呢?
例如对于\(A(1,1)\)这个点,我们在它的左右各取一个点B、C,并逐渐靠近它:
PS: 从这里我开始尝试使用 GeoGebra 来作图,网页版的画图实在是太!蛋!疼!了!。。
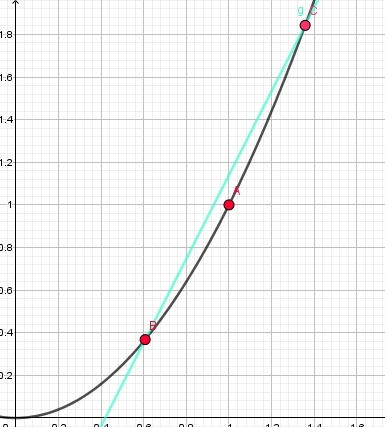
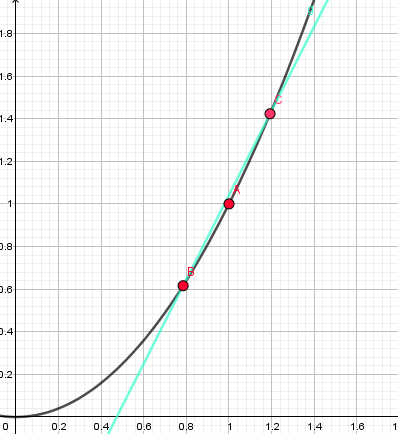 就这样不断靠近靠近。。
就这样不断靠近靠近。。
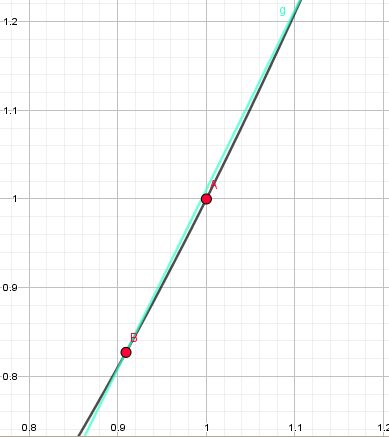
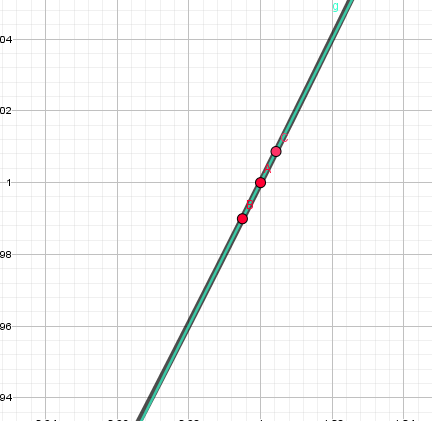 终于,在N+N次逼近A点后,三个点几乎实现了重合:
终于,在N+N次逼近A点后,三个点几乎实现了重合:
 注意,我这里之所以强调几乎,是因为它们确实没有碰上,只是它们之间的距离已经微小到了无穷的小。
注意,我这里之所以强调几乎,是因为它们确实没有碰上,只是它们之间的距离已经微小到了无穷的小。
此时,我们仍然能作直线\(BC\),我们就称这条直线为点\(A\)在函数\(y=x^2\)上的切线。
好了,讲了这么多,我们可以回到原来的话题了。点A的斜率是多少?我相信,你已经心中有数了吧。
二次函数图像上的点A的斜率就是点A在这个函数图像上的切线的斜率。
这句话初看有点儿像句绕口令,多看几次才能搞明白。
(假设你已经看明白了,如果没有,你就假装看懂了 :) )
OK,那么接下来,让我们正式开始导数的学…哦不!可能还要加点料才行….
1.3 极限?
在介绍导数之前,我们还得弄懂另外一个概念:极限。 极限,顾名思义,就是到达了极点的状态。比如说,考试还有1分钟就要结束时题目还没有答完时的感觉,或者暑假开学前的晚上猛补作业时的感受。人们在遇到极限时通常都会想:“不行了!不行了!”
但是,数学中的极限也是这个意思吗?如果指”不行了”“到头了”,又怎么能解决数学问题呢? 事实上,数学中的极限的含义更加积极,它有”尽可能靠近”的意思,也就是无限地靠近。 由于是数学,自然离不开数值了…所以,极限就是指一个数值尽可能地向另一个数靠近。
啥叫”尽可能地靠近”?举个例子,小明的家距离学校1000m,某天小明去上学,于是他与学校的距离变化如下:
1000m
∨
500m
∨
200m
∨
100m
∨
1m
∨
0.1m
∨
0.01m
∨
0.0000000000001m
...
∨
0.0000000000000000000000000001m
可以看到,小明与学校之间的距离越来越小,越来越靠近于 0m,但是就是到达不了 0m(因为他不想上学),于是我们就可以说
\[\lim_{距离 \to 0 m}\]
突然给出这么一个数学式子,你可能会一脸蒙蔽:这是个啥?
查查英汉词典可得知:Lim 原来是 Limit 的缩写,而 Limit 就是「极限」的意思。下面的小字里的「\(\to\)」表示「向 xxx 靠近」,所以这里的意思是”让 距离 这个值给我向 0m 尽可能地靠近!”
上面这个式子就表示距离 无限地向\(0\ m\)靠近(但是就是到达不了\(0\ m\)!)
OKOK,理解了,那么让我们在式子上再加点花样吧!
\[\lim_{x \to a} f(x)=b\]
诶…更晕了…你可能会想:「这东西…现在我连符号都看不懂了!」
别急,让我再给你挨个儿解释解释!
首先看这个\(f(x)\),这里的\(f\)是啥意思呢?其实很简单,f是单词“function”开头第一个字母,“function”就是函数的意思,所以\(f\)就是指某个函数。比如说一次函数,在初中学习中我们表示成
\[y=2x\]
想表示\(x=1\)时的值,我们得说
\[当x=1时,y=2\]
但是到了高中数学以及高等数学中,因为这样写起来太麻烦了,所以同一个函数,我们表示成
\[f(x)=2x\]
想表示\(x=1\)时的值,就可以简练地写成
\[f(1)=2\]
是不是很方便?
(顺便说一句,这里不一定必须用\(f\)作为函数的标识,如果你喜欢,也可以写
\[我真是酷毙了(x)=2x,我真是酷毙了(1)=2\]
)
回到上面的式子。\(f(x)\)就是以x为自变量的某个函数,在这里它到底是什么,我们不管它。
继续往下,下面的”\(x \to a\)“意思应该是”自变量x向a无限地靠近”。
这样,这个式子我们至少弄懂一半了,\(\lim_{x \to a} f(x)\)就是表示”对于\(f(x)\)这个函数,让\(x\)无限地逼近\(a\)“。
奇怪的是,式子的后面居然出现了等于号…小明上学时,与学校的距离也是一直在不停地变小啊…如果说是无限靠近\(a\),又哪来的等于不等于呢?难道\(f(x)\)这么神奇,可以一边靠近,一边等于某个值吗?
这里就要提醒一下了:含有\(lim\)的式子里,所有”\(=\)“的意思都有一点小小的变动,不再表示”等于什么”,而是“靠近什么”。
所以啊,上面这个式子表示“当\(x\)无限地靠近\(a\)的时候,\(f(x)\)无限地靠近\(b\)”。
啪啪啪!第一个奇怪的数学符号,终于是被我们弄明白了!
1.3.1 小练习
稍微弄几道关于极限的题来做做吧…我们来找找感觉。
第一题
\[\lim_{x \to 1} x=?\]
唉…没什么难度嘛,直接把1代入进\(x\)算一下,结果就是\(1\)。
第二题
\[\lim_{x \to 3} x^2=?\]
稍微需要一点计算了,\(3^2=3*3=9\),所以答案是\(9\)。
第三题
\[\lim_{x \to 0} (2x^2+5x+8)=?\]
似乎和第二题差不多么,只是计算有点麻烦了,列个式子算一下,\(2x^2+5x+8=2*0^2+5*0+8=8\),结果是\(8\)。
第四题
你可能纳闷:这和一般的函数计算有什么区别?从哪里能体现出这个\(lim\)的特殊性?
来看这题:
\[\lim_{x \to 1} \frac{x^2-3x+2}{x-1}=?\]
妈呀,这题好像不能代入计算了?难道答案是\(\frac2 0\)吗?
不可能,分数的分母不能为0的…
那要怎么算呢?没有结果吗?
实际上,我们发现这个式子可以因式分解:
\[\frac{x^2-3x+2}{x-1}=\frac{(x-2)(x-1)}{x-1}=x-2\]
所以上面的题目就相当于
\[\lim_{x \to 1} (x-2)=?\]
答案就是\(-1\)。
这里你可能会说:\(x-1\)既然为0了,又怎么能约分上面的分数呢?
我们需要再看一遍极限的概念:一个数值尽可能地向另一个数靠近。这里的\(x-1\)准确地说,应该是一个非常非常接近于0,但不是0的值,所以是可以约分的。
这里用到了因式分解的技巧,算是比较麻烦的一题,我们暂时搁下,不深入讨论了。
1.3.2 额外的问答时间
你可能还有一些问题..让我尝试解答一下。
问:为什么代入数值,求得的就是它的极限呢?有什么理论依据吗?
答:这个问题比较难以解释,需要牵扯到函数的连续性之类的。我们还是按下不表,以免影响了本文的易懂性。
问:上面说极限的格式是 \(\lim\limits_{x\to a} f(x)=b\),怎么后面又写成 \(\lim\limits_{x\to 1} x=1\) 了呢?
答:格式里给出的写法是大概的、通用的写法,实际使用中我们不会写成
\[f(x)=x,\lim\limits_{x \to 1} f(x)=1\]
这么麻烦,直接用\(x\)代替极限格式中的\(f(x)\),其潜台词也就是默认\(f(x)=x\)了。
1.4 斜率的计算
嗯,讲完了斜率的画法和极限的概念,我们可以综合一下这两个知识,开始真正的导数之旅了。
我们来看看斜率到底是怎么算出来的。
 我们仍然以这个函数图像\(f(x)=x^2\)为例。
我们仍然以这个函数图像\(f(x)=x^2\)为例。
如果我们设A点的坐标为\((x,f(x))\),那么C点坐标可以表示成\((x+h,f(x+h))\) (h是某个值),这没问题吧?
那么
\[AC的斜率=\frac{C点纵坐标-A点纵坐标}{C点横坐标-A点横坐标}\]
如果你看到这个式子感到一脸懵,那么你得重新看看这张图了:
 一次函数的斜率是某两点的竖直高度差除以水平高度差。类似地,AC的斜率我们也可以这么写。
一次函数的斜率是某两点的竖直高度差除以水平高度差。类似地,AC的斜率我们也可以这么写。
继续我们的计算:
\[AC的斜率=\frac{C点纵坐标-A点纵坐标}{C点横坐标-A点横坐标}=\frac{f(x+h)-f(x)}{(x+h)-x}=\frac{f(x+h)-f(x)}{h}\]
这样,我们就得到了两点之间的斜率公式。
再进一步想想,我们要求出的是点A的斜率,光有两点的斜率公式要怎么办呢?
不管三七二十一,咱们先把数值代进式子里面再说。A点的坐标是(1,1),所以有
\[AC的斜率=\frac{f(1+h)-f(1)}{h}\]
这个式子看起来还是没法算啊…让我们稍微再化简一下,可以发现\(f(1)=1^2=1,f(1+h)=(1+h)^2\)。
所以这个式子还可以进一步化简:
\[AC的斜率=\frac{f(1+h)-f(1)}{h}=\frac{(1+h)^2-1}{h}\]
根据刚学到的完全平方公式,还可以再展开:
\[AC的斜率=\frac{(1+h)^2-1}{h}=\frac{h^2+2h+1-1}{h}=\frac{h^2+2h}{h}=h+2\]
这里的\(h\)是多少呢?
刚才讲到,\(h\)表示的是A点与C点横坐标的距离。而这两点,在前面就说到是非常非常接近的,所以\(h\)应该是一个很小很小的值。
很小很小…很接近很接近…有没有觉得这两句话有点熟悉?
。
。
。
。
。
。
。
。
。
。
。
。
。
没错!就是在 极限? 这一节里,我们简要地讲了如何正确处理数学里很接近的值。
关键的地方来了!\(h\)既然很小,我们就可以把上式加上\(\lim\)写成:
\[AC的斜率=\lim_{h \to 0}(h+2)\]
然后,后面这个式子的计算方式已经略熟悉啦,直接算出
\[AC的斜率=\lim_{h \to 0}(h+2)=2\]
这样,我们就终于得出了点A(1,1)在\(f(x)=x^2\)上的切线AC的斜率,也就是点A(1,1)在\(f(x)=x^2\)上的斜率。
看起来,计算一个点的斜率也没那么困难嘛!
1.4.1 小结
上面求斜率的过程可以概括成这几步:
- 在要求斜率的点\((x,f(x))\)附近找出一个与它很靠近的点\((x+h,f(x+h))\)!
- 把斜率用\(\frac{C点纵坐标-A点纵坐标}{C点横坐标-A点横坐标}\)表示出来!
- 在式子前面加上\(\lim_{h \to 0}\),代入进去计算斜率!
1.4.2 通式
从上面的过程中我们可以看出,求某个点的斜率有固定的步骤和方法。依照这个方法,理论上来说我们可以求出任何函数上点的斜率。
接下来让我们试着找出这样一个公式,来表示任何函数\(f(x)\)上任意的点\((x,f(x))\)的斜率,这样,以后进行计算时就很方便了。
这个过程并不困难。让我们用\(f(x)\)来代替上面的\(1\)就可以了。
\[斜率=\lim_{h \to 0}{\frac{f(x+h)-f(x)}{(x+h)-x}}=\lim_{h \to 0}{\frac{f(x+h)-f(x)}{h}}\]
这就是任意函数在某一点的一般斜率公式。
呼,讲了这么多废话,我们总算开始步入正轨,而不是在各种概念上原地打转了。(哈哈)
记不住完整的公式也不要紧,需要用到的时候现场推导就可以了,理解这个有点复杂的式子才是关键。
1.4.3 求斜率有什么用?
我们已经基本掌握了求某一个点的斜率的方法。那么,这个东西有什么用处呢?
毕竟,如果没有实际用途的话,这样的数学工具看起来也没有什么意义啊…
在求导的用途中,最重要的也就是求某一点的切线的函数式。
因为用导数可以得出某一点的斜率,把斜率作为\(k\)代入\(f(x)=kx+b\),很方便地能求出该点的切线方程。
实际上,在本文中我们就是用”某一点切线的斜率”来定义”某一点的斜率”的,是不?
依然以上面一节中的\(f(x)=x^2\)和点\(A(1,1)\)为例,我们来求一下A点的切线方程。
已经知道A点的斜率为2了,所以立即有
\[g(x)=2x+b\]
是A点的切线方程。
又知道这个方程经过A点,故使用待定系数法:
\[g(1)=2*1+b=1\]
解得
\[b=-1\]
所以A点的切线方程就是
\[g(x)=2x-1\]
这个结果对不对?画出来看看就知道有没有问题了。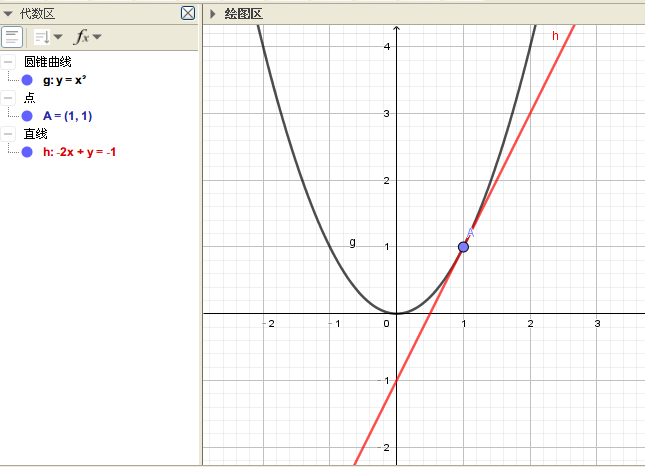 图中红色的线就是我们刚刚求出的直线。看起来它的确是A点的切线。
图中红色的线就是我们刚刚求出的直线。看起来它的确是A点的切线。
另一个用途是求函数的最大/最小值。容易看出,上面这个函数的顶点\(O(0,0)\)的斜率为0。
因为顶点有”这一点的前后既不在上升,也不在下降”的性质,所以顶点的斜率都应该是0。
也就是说,只要找到一个函数中有一个斜率为0的点,就可以确定这一点是函数的一个顶点。
在接下来的 导函数 一节里,我们会讲得更多。
1.5 导函数
了解了导数和函数,这个”导函数”是个什么东西啊?别急,听我慢慢道来。
再看一眼这个式子:
\[\lim_{h \to 0}{\frac{f(x+h)-f(x)}{h}}\]
其实,这个式子就是\(f(x)\)的导函数。
函数是什么?我们复习一下函数的定义:
设A,B是非空的数集,如果按照某种确定的对应关系f,使对于集合A中的任意一个数x,在集合B中都有唯一确定的数\(y\)和它对应,那么就称映射\(f:x\to y\) 为从集合A到集合B的一个函数,记作\(y=f(x)\)。
不好意思拿错了,是这个:
在一个变化过程中,假设有两个变量x、y,如果对于任意一个x都有唯一确定的一个y和它对应,那么就称x是自变量,y是因变量,y是x的函数。
也就是说,只要有一个对应关系f,就可以说f是个函数。 函是”匣子”的意思。把一个数\(x\)装进一个匣子,按照某个算式计算出另一个数字,就是函数。
因此,对f(x)求导的式子也是函数。 这个函数,对于每一个x,计算出的结果都是\((x,f(x))\)在\(f(x)\)上的斜率。需要求导的时候,我们就不用对每个数字都重新列式求一遍了,直接代入导函数就行,很方便。
导函数一般记作\(f^{\prime}(x)\)。
继续以\(f(x)=x^2\)为例,我们看看它的导函数长什么样子。
这次我们不代入任何值,直接运用上面的公式:
\[f^{\prime}(x)=\lim_{h \to 0}{\frac{f(x+h)-f(x)}{h}}=\lim_{h \to 0}{\frac{(x+h)^2-x^2}{h}}\]
然后是
\[=\lim_{h \to 0}{\frac{x^2+2xh+h^2-x^2}{h}}=\lim_{h \to 0}{\frac{2xh+h^2}{h}}\]
最后
\[=\lim_{h \to 0}(2x+h)\]
又因为h靠近0,所以直接舍去,得到:
\[=\lim_{h \to 0}(2x+0)=2x\]
所以\(f^{\prime}(x)=2x\)。
仔细观察这个式子,我们发现它很有特点。
比如说想求\(A(1,1)\)斜率,我们也不用重新计算了,直接用导函数就行了。
\[A的斜率=f^{\prime}(1)=2\]
同理,想求\(B(2,4)\)斜率的话:
\[B的斜率=f^{\prime}(2)=4\]
是不是很方便?
导函数本身也是函数。所以对导函数\(f^{\prime}(x)\)求导还可以得到另一个函数,称为二阶导数,一般记作\(f^{\prime\prime}(x)\)。
当撇号过多时,比如说有个99999阶导数,直接记作\(f^{(99999)}(x)\)即可,不用打撇号了。
导函数有什么意义?只是为了装逼吗?
在了解这个问题之前,先想想导函数\(f^{\prime}(x)\)和函数\(f(x)\)之间的区别和联系。
| 项目 | \(f(x)\) | \(f^\prime(x)\) |
|---|---|---|
| \(x\)对应的函数值\(y\) | 是函数的值 | 是函数\(f(x)\)的图像上,横坐标为\(x\)的这一点的求导结果 |
| 是否是函数 | 是 | 是 |
| 求导结果 | \(f^\prime(x)\) | \(f^{\prime\prime}(x)\) |
| 函数零点的意义 | 无特殊意义 | 是\(f(x)\)的顶点的横坐标 |
(注:零点:函数的零点就是\(函数=0\)这个方程的解。 比如\(f(x)=x^2-1\)的零点就是\(x^2-1=0\)的解,也就是\(1\)和\(-1\) 。)
所以,导函数有一个重要的作用,就是计算函数的顶点坐标。
由于顶点的特殊性,该点的斜率是0,所以只要找出导函数\(f^{\prime}(x)\)的零点,相当于找到了顶点。
以\(f(x)=ax^2+bx+c\)为例。它求导的结果是\(f^{\prime}(x)=2ax+b\)。
\(f^{\prime}(x)=0\)的解就是\(x=-\frac{b}{2a}\)。这是不是与你在课堂上学到的二次函数的最值完全一致?
导函数的另一个作用是画函数草图。
前面已经说过,如果导函数\(f^{\prime}(x)>0\),说明函数在这一点上的斜率是正的,也就是说,在这一点的前后,函数应该呈上升的趋势。
相反,如果\(f^{\prime}(x)<0\),说明函数在这一点上的斜率是负的。在这一点的前后,函数应该呈下降的趋势。
于是乎,只要搞明白\(f^{\prime}(x)\)的图像,就可以把\(f(x)\)的图像画出来了。
举个例子,如果我们要画\(f(x)=x^2+2\)的草图,我们可以结合导函数这么画:
- 求导,得到\(f^{\prime}(x)=2x\).
- 画出\(f^{\prime}(x)=2x\)的图像。

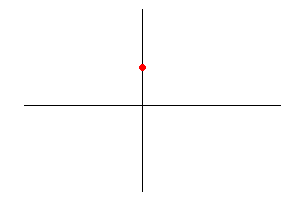
- 准备开始画图!先找出一个起点,这里我们取\(f(0)\)这一点,也就是\(A(0,2)\)。

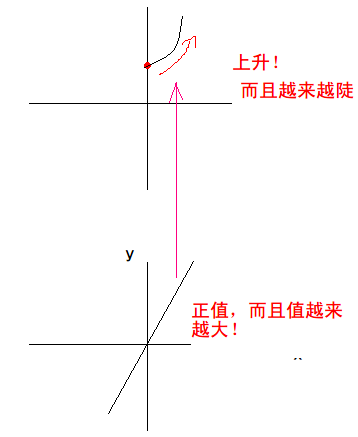
- 按照\(f^{\prime}(x)\)的图像所示,y轴的右边应该都是上升的,而且斜率越来越大,也就是:

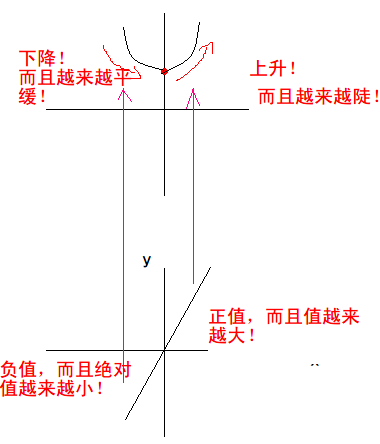
- 同理,画出左半边:

这样就把\(f(x)=x^2+2\)的图像大概描出来了。
这题中导函数的优势还不能充分体现出来。遇到一些比较复杂的函数,一般结合导函数这样画图比较方便。
1.5.1 导数的表示方法
前面说到,导函数一般记作\(f^{\prime}(x)\)。
但是,实际上导函数还有一些常见的表示方法,这里介绍两种,以备后面的装逼使用。
第一种也就是刚刚讲的加撇号表示法。这种方法是在19世纪,一个叫 约瑟夫·路易斯·拉格朗日 的法国大叔发明的。
在他的表示法里,\(y=f(x)\)的导函数记作\(f^{\prime}(x)\)或者\(y^{\prime}\)。
这种表示方法非常常见,因为它写起来很容易,加个撇号只要花上你半秒钟的时间。
但是,它的弊端在于,如果有这么一个函数:
\[y=a+b\]
那么\(y^{\prime}\)表示什么?
\(a\)和\(b\),到底谁才是自变量?谁是常量?
到底\(y^{\prime}\)表示是对\(a\)求导,还是对\(b\)求导?
不得而知。
要是有一种表示方法可以体现出对谁求导就好了。
这时,我们就需要第二种表示方法,也就是 戈特弗里德·威廉·莱布尼茨 ,另一个德国大叔的写法。他也是微积分的主要创始人,他生活在17世纪,比上面那位要早几百年。
对\(y=f(x)\)关于\(x\)求导可以表示成:
\[\frac{dy}{dx},\frac{d}{dx}y,\frac{df(x)}{dx},\frac{d}{dx}f(x)\]
这些式子看起来很让人头晕…
(正因如此,他的符号至今仍在大学数学中频频现身。)
这里的\(d\)是Derivative(导数)的首字母。
式子的含义是对分母上的自变量,求分子上的函数的导数。
其中,\(\frac{d}{dx}\)可以看成是一个整体,它乘以谁,就是对谁求导。
例如:
\[\frac{d}{dx}x^2=2x\]
所以,如果我们想要表示导数的导数,也就是\(f^{\prime\prime}(x)\),要怎么写呢?
就是:
\[f^{\prime\prime}(x)=\frac{d}{dx}\times\frac{d}{dx}\times y=\frac{d^2y}{dx^2}\]
分子上加平方的位置看起来怪怪的。而且d似乎也不遵循乘法定律。
你可能觉得莱布尼兹的方法很麻烦,但是在后面的章节里,你会逐渐明白这样表示的优点。
1.5.2 小结&补充
到现在为止,我们已经学会了:
斜率是什么&怎么算导数是什么&怎么求导函数是什么&怎么求
你可能还没有完全掌握以上内容,那也没关系!~
接下来我们会给出一些简单实用的公式,在你的学习过程中会频繁地使用它们来避免复杂的运算过程。一定要记牢!~
\[b^\prime=0\]
\[x^\prime=1\]
\[(kx)^\prime=k\]
\[(kx+b)^\prime=k\]
\[(ax^n)^\prime=anx^{n-1}\]
以上就是最基础的一组导数公式,其中\(a和b\)的含义是任意常数。
记住了它们,即使不会推算导数也可以轻松求出初高中大部分函数的导函数!
尤其是最后一个,堪称初等函数大杀器…
举个例子,要求出\(y=2x^{999}\)的导函数,直接用上面的公式:
\[y^{\prime}=2*999*x^{999-1}=1998x^{998}\]
是不是贼方便?
[选读]这里还有一些为学过三角函数的同学补充的:
\[(sinx)^\prime=cosx\]
\[(cosx)^\prime=-sinx\]
\[(tanx)^\prime=\frac{1}{(cosx)^2}\]
1.5.3 五年高考,三年模拟(雾)
总觉得应该来几道题目练练手…
虽然这样有点像老师上课的模式,有悖本文的初衷,但是练习一下真的能掌握不少…
废话少说,放题过来!
 。
。
。
。
。
。
。
。
。
- 求出\(f(x)=x^4-2x\)的导函数。
- 求出\(f(x)=(x+2)^{11}\)的导函数。
- 求出\(f(x)=x^{x}\)的导函数。
- 求出\(f(x)=\sqrt{x}\)的导函数。
- 求出\(f(x)=\sqrt[x]{x}\)的导函数。
- 求出\(f(x)=\sqrt[sin(x)]{x^{cos(x)}}\)的导函数。
- 对于以上题目,你有什么感想?
作者的话:最近学业方面实在比较忙,先是期中考,又是统考月考周考什么的,今天刚参加全省联考…..(高二狗,体谅一下)说好的两个月完工也没下落了:(
2021年9月24日更新:作者回来啦!现在已经是一条大二狗了,国庆期间会重启更新~
1.5.4 导函数的四则运算
上面那几题已经让你晕头转向了?没关系!看完本节和下一节之后,你将可以很快地计算出它们从而去装B!
迄今为止,我们提到的例子都是一些比较简单的函数(额,当然上面的几题除外)。
基本上函数里都只有一个\(x\)。形式也就是\(x+1\),\(x^2\)这样的,大家都学过了。
但是,平时遇到的函数可没这么简单,数学考试里当然不会直接出这样的玩意儿来考你。即便刚刚学过二次函数,你也应该已经遇到\(f(x)=x^2+3x+2\)或者\(f(x)=(x-2)^2+3\)这样的函数了。这种东西要怎么求导数呢?
其实很简单!不妨回忆一下下我们上面提到过的例子:
以\(f(x)=ax^2+bx+c\)为例。它求导的结果是\(f^\prime(x)=2ax+b\)。
(限时挑战任务!看看你能不能在 10 秒内找到这句话的出处:) )
我们先不管结果是啥,只看每个部分。这个式子的每一部分我们都会求。\(ax^2\)的导数就是\(2ax\),\(bx\)的导数就是\(b\),\(c\)的导数……呃呃,一个常数的导数,永远是\(0\)嘛。
所以……它的导数就是\(2ax+b\)?看起来确实是这样。
我们不妨大胆猜测一下:求一个里面有加号的函数的导数,只要求出各个部分的导数,然后加起来就好啦!
然而事实是怎样呢?事实是……我们的猜测是对的。导数的加法就是可以这么拆开计算的。
写成公式的方式就是:
\[(A+B)^\prime=A^\prime+B^\prime\]
(别忘了一撇「\(\prime\)」的含义哦,它是指对这个式子求导。)
那么,这是为啥呢?这个问题我们稍微往后放放,你在后面的选读部分会看到它的证明。
我们先看看利用这个,能不能做出上面的题了。
第一题是\(f(x)=x^4-2x\)。
它的第一部分求导是\(4x^3\)(别忘了这个公式哟:\((ax^n)^\prime=anx^{n-1}\)),第二部分的导数是\(2\)。所以结果就是\(4x^3+2\)。
第二题是\(f(x)=(x+2)^{11}\)……额,这个怎么办呢?
其实只要一点一点乘开就好了!打开我们的 Maple,输入函数,点击展开:
 然后按上面的方法,对每个部分求导就好了!
然后按上面的方法,对每个部分求导就好了!
你可能会说:\((x+2)^{11}=(x+2)(x+2)(x+2)(x+2)(x+2)...\),这么长的式子,考试的时候要展开不得累死我?
当然,这种暴力算法虽然不能实用,但是至少是可以算出来的。如果遇到这样的函数,展开是最差劲的选择,但起码是一种选择……起码是可以算出来的,是吧?
这种方法显然太蠢了。有没有更妙的方法来计算第二题呢?这就进入到咱们今天的重头戏:复合运算!
。
。
。
诶还没进呢,没看到标题是「四则运算」吗?等下一节吧(顶级拉扯)
加法已经说完了,我们来看看乘法吧。
(大家读到这里可能比较突兀,因为上面的练习里面忘了出相关的题了。偏偏这个乘法运算又很重要,还是希望大家快速过一遍!不要跳过哈,不然你待会儿会后悔的,哼哼)
什么叫乘法运算呢?举个例子:
\[f(x)=(x^3+3x+3)(x^2+2x+2)\]
这个函数怎么求导呢?有同学可能会说:加法是分开加,那我乘法也分开乘嘛!先对\(x^3+3x+3\)求导,再对\(x^2+2x+2\)求导,然后乘起来就好了吧?
但是,But,这样是完全错误的哦!不如再想想?先乘开自己求导一下,再找找规律?
算啦算啦,我知道你很想知道,先把正解放在这里:
\[f^\prime(x)=(x^3+3x+3)^\prime(x^2+2x+2)+(x^3+3x+3)(x^2+2x+2)^\prime\]
\[=(3x^2+3)(x^2+2x+2)+(x^3+3x+3)(2x+2)\]
这就是说,乘法的规则和加法完全不同,它的导数是对第一个式子求导,乘第二个;再对第二个式子求导,乘第一个。然后加起来。
写成公式的方式就是:
\[(AB)^\prime=AB^\prime+A^\prime B\]
或者写得再「专业」一点:
\[(f(x)g(x))^\prime=f^\prime(x)g(x)+f(x)g^\prime(x)\]
先尝试理解一下这个式子哈。
我知道你的心里肯定装满了大大的问号:凭啥这么算?你这是个啥计算方法?你这样算出来,真的是对的嘛?
很不幸的是,它确实是对的。凭什么呢?
这就有点超过知识范围了。
我一起放在下面的选读部分吧,如果你自认为可以,不妨挑战一下阅读!应该……不会需要太高的数学水平?(这个挑战就没有上面的「习题」那么坑了,哈哈!)
[选读] 加法求导公式的证明
要证明对两个函数\(f(x)\)和\(g(x)\),可以推出\((f(x)+g(x))^\prime=f^{\prime}(x)+g^{\prime}(x)\)。
先回顾公式:\[f^{\prime}(x)=\lim_{h \to 0}{\frac{f(x+h)-f(x)}{h}}\]
,
所以写出\((f(x)+g(x))^\prime\)的求导式子,然后摆弄一下式子的加法顺序:
\[\begin{aligned}(f(x)+g(x))^\prime\\&=\lim_{h \to 0}{\frac{(f(x+h)+g(x+h))-(f(x)+g(x))}{h}}\\&=\lim_{h \to 0}{\frac{f(x+h)+g(x+h)-f(x)-g(x)}{h}}\\&=\lim_{h \to 0}{\frac{(f(x+h)-f(x))+(g(x+h)-g(x))}{h}}\\&=\lim_{h \to 0}{\frac{f(x+h)-f(x)}{h}}+{\frac{g(x+h)-g(x)}{h}}\\&=f^{\prime}(x)+g^{\prime}(x)\end{aligned}\]
这就证完了!
[选读] 乘法求导公式的证明
要证明对两个函数\(f(x)\)和\(g(x)\),可以推出\((f(x)g(x))^{\prime}=f^{\prime}(x)g(x)+f(x)g^{\prime}(x)\)。
还是写出\((f(x)g(x))^{\prime}\)的求导式子:\[(f(x)g(x))^{\prime}=\lim_{h \to 0}{\frac{f(x+h)g(x+h)-f(x)g(x)}{h}}\]
呃,这里不太好办了……只有两项,怎么玩它呢?
其实可以试试「凑项」!具体来说,就是加一个什么东西,再减去它,这样式子依然不会变,就像\(123+1-1\)还是\(123\)一样!我们这里要凑进去的是\(f(x+h)g(x)\),详细地说就是凑成下面这样:
\[\begin{aligned}(f(x)g(x))^{\prime}\\&=\lim_{h \to 0}{\frac{f(x+h)g(x+h)-f(x)g(x)}{h}}\\&=\lim_{h \to 0}{\frac{f(x+h)g(x+h)-f(x+h)g(x)+f(x+h)g(x)-f(x)g(x)}{h}}\\&=\lim_{h \to 0}{\frac{f(x+h)(g(x+h)-g(x))+(f(x+h)-f(x))g(x)}{h}}\\&=\lim_{h \to 0}{f(x+h)\frac{g(x+h)-g(x)}{h}}+\frac{f(x+h)-f(x)}{h}g(x)\\&=f(x+h)g^{\prime}(x)+f^{\prime}(x)g(x)\end{aligned}\]
注意,h是无限趋近于0的,所以上式也就是\(f(x)g^{\prime}(x)+f^{\prime}(x)g(x)\)了。
PS:这两个证明乍一看很麻烦,但是自己动手写一遍,你会发现还挺简洁的……
2023年2月13日更新:啊,迟来的更新!
到这里为止,我们已经介绍了含有加法和乘法的导数计算,总结一下:
- 对于加法,我们可以用加法求导公式: \(\begin{aligned}(f(x)+g(x))^\prime&=f^{\prime}(x)+g^{\prime}(x)\end{aligned}\);
- 对于乘法,我们可以用乘法求导公式:
\(\begin{aligned}(f(x)g(x))^{\prime}&=f^{\prime}(x)g(x)+f(x)g^{\prime}(x)\end{aligned}\)。
接下来是减法和除法。加法和减法是一对同胞兄弟,掌握了带加法的求导,带减法的求导就非常顺理成章了:
\[(f(x)-g(x))^\prime=f^{\prime}(x)-g^{\prime}(x)\]
为什么是这样呢?因为减法可以转化为加法,比如\(3-2=3+(-2)\),所以和加法的求导公式非常类似,只不过是把加号换成了减号而已。
更严格的证明可以这么想:利用负数,我们就可以把减法全部变成加法:
\[f(x)-g(x)=f(x)+(-1)\times g(x),\]
而这时就可以利用加法求导公式了。
如果你问 \(\left[(-1)\times g(x)\right]'\) 是什么,不妨再看看 1.5.2 节给你的简单实用的公式?
(然后你就会知道 \(\left[(-1)\times g(x)\right]'=-1\times g'(x)=-g'(x)\) 了。要时常回顾之前学过的东西哦!)
只要利用一下加法求导公式,其实就已经得到上面的减法求导公式了。这样,四则运算里的三个求导公式就都证明完了!
然而,除法这个看起来平平无奇的运算,求导却是最难的。为了证明它,上面所有的知识甚至都还不够,我们还需要用到一个(刚刚提了一嘴的)新概念:复合函数。下一节我们就来讲讲复合函数和它的求导。
1.5.5 复合函数的导函数
你也许火急火燎地翻过了上面的证明,想要知道复合函数的求导公式是什么。在了解求导公式之前,我们先来看看复合函数是什么。
最直观地说,复合函数就是把一个函数「塞」到另一个函数里面去,然后把它们合并成一个新的函数。
比如,我们把函数\(f(x)=x^2\)「塞」到函数\(g(x)=x+1\)里面去,就得到了一个新的函数\(h(x)=g(f(x))=x^2+1\)。这个新函数\(h(x)\)就被称为\(f(x)\)和\(g(x)\)的复合函数。
这里,\(f(x)\)替代了\(g(x)\)的式子里的\(x\)的位置,所以才写成了\(g(f(x))\)。意思就是:\(g\)这个因变量,它的自变量现在不叫\(x\)了,而是全部替换成\(f(x)\)。既然 \(g(x)\) 是
\[g(x)=x+1,\]
那\(g(f(x))\)的式子理应是:
\[g(f(x))=f(x)+1.\]
既然 \(f(x)=x^2\),那么\(g(f(x))\)的式子就进一步可以代换成:
\[g(f(x))=x^2+1.\]
有人可能会问:你把自变量从\(x\)换成了\(f(x)\),那原来的因变量 \(g\) 不就变了吗?这么说对也不对。
[提示]
下面这一部分是对函数的深入讲解,如果你觉得有些难以理解,可以先跳过,等到后面再回来看。
在高等数学里,我们不再提「因变量」和「自变量」这两个概念了,而是用「函数」和「变量」来代替。函数的括号里一定是一个字母吗?未必。函数括号里的就得是一个变量吗?也未必。我们已经见过很多种写法:
- \(f(x)\):代表一个函数,它的自变量是\(x\);
- \(f(1)\):代表令函数\(f(x)\)的自变量\(x\)等于1时的函数值;
- \(f(g(x))\):代表令函数\(f(x)\)的自变量\(x\)等于另一个函数\(g(x)\)时的函数。
说白了,函数只是一个黑盒子,你不清楚里面的计算过程,只能往里面塞一个东西,然后得知它计算出的东西。
它的括号里是你可以塞进去的东西,你想塞什么都可以。你塞进去一个变量 \(x\),根据计算结果就知道这个函数和 \(x\) 有什么关系了;你塞进去一个函数 \(g(x)\),根据计算结果就知道这个函数和 \(g(x)\) 有什么关系了;你塞进去一个值 \(1\),根据计算结果就知道这个函数和 \(1\) 有什么关系了。
注意,这里的「计算结果」并不一定和你塞进去的东西直接有关系。不是说你塞进去值就一定得到值,也不是说塞进去变量就一定还是函数。比如这个函数:\(f(x)=x^2+y\)。把 1 塞进去,你会得到:
\[f(1)=1^2+y=1+y.\]
你可能会奇怪:\(f(1)\) 怎么不是一个数字,而是含有一个未知字母 \(y\) 的式子呢?这也能被称为一个函数吗?答案是:当然可以。函数这个黑盒子只能保证两条规则:
- 你塞进去一个未知量,就一定能得知黑盒子的全貌。比如你塞进去一个变量 \(x\),就能得知这个函数和其他任何量有什么关系,也清楚明白地知道黑盒子的运作原理了:\(f\) 其实就是把塞进去的东西平方,然后再加上一个未知量 \(y\) 嘛!
- 它计算出的东西一定是一个式子。当然,这个式子里可能有整数,有小数,有加减乘除,甚至有未知量,但它一定是一个式子。除此之外,函数不会给你任何保证。你塞进去一个值,它或许会给你一个值,也或许会给你一个式子。
这就是为什么我们可以写出\(g(f(x))\)这种东西的原因。\(g\)是一个黑盒子,我们把\(f(x)\)塞给它(或者说,把\(x^2\)塞给它),它根据和塞给它\(x\)时一样的工作原理,计算出了一个式子。这个式子里有一个未知量 \(x\),所以我们说\(g(f(x))=x^2+1\)。
回归正题,讲讲复合函数的求导。这个求导公式是:
\[\left[g(f(x))\right]'=g'(f(x))f'(x).\]
这个公式的意思是:复合函数的导数等于里面的函数的导数乘以外面的函数的导数。
啊,又是一个和乘法求导公式一样拗口的公式!
[选读] 复合函数求导公式的证明
它的证明过程也是很复杂的,考虑到网上两三步证完的基本都是错误证明(包括高中课本上的),而在严格的分析法里需要考虑诸多细节,可能你也不想看(即便是高中数学水平,硬着头皮也未必能看懂),所以这里只能扔个链接给你:复合函数求导公式的证明,如果闲着没事,可以看看。
PS:说复杂,其实也不复杂,主要是有很多边边角角的情况需要分类讨论,每一种单独证明,因此汇成了一篇长篇大论……
不过,这个公式的意思其实很简单。我们继续说上面\(f(x)=x^2, g(x)=x+1\)的例子。要分几步走来计算:
- 先计算\(f(x)\)的导数,得到\(f'(x)=2x\);
- 再计算\(g(x)\)的导数,得到\(g'(x)=1\);
- 然后计算\(g'(f(x))\),得到\(g'(f(x))=1\)(因为 \(g'(x)\) 是一个常函数,你把 \(x\) 换成任何值,它都给你 \(1\)!);
- 最后,计算\(g'(f(x))f'(x)\),得到\(g'(f(x))\times f'(x)=1\times 2x=2x\);
- 所以,最终的答案是\(\left[g(f(x))\right]'=2x\)。
这个结果和我们直接对\(g(f(x))=x^2+1\)等式右边的\(x^2+1\)求导数的结果是一样的。
现在,让我们再试试前一节的问题:\((x+2)^{11}\)的导数是多少?我们可以把它拆成复合函数的形式:
\[f(x)=x+2, g(x)=x^{11},\]
那么\(g(f(x))\)就是\((x+2)^{11}\)。这下我们只要计算\(g(f(x))\)这个复合函数的导数就可以了:
- 先计算\(f(x)\)的导数,得到\(f'(x)=1\);
- 再计算\(g(x)\)的导数,得到\(g'(x)=11x^{10}\);
- 然后计算\(g'(f(x))\),得到\(g'(f(x))=11(x+2)^{10}\);
- 最后,计算\(g'(f(x))f'(x)\),得到\(g'(f(x))\times f'(x)=11(x+2)^{10}\times 1=11(x+2)^{10}\);
- 所以,最终的答案是\(\left[g(f(x))\right]'=11(x+2)^{10}\)。
这样,我们就把复合函数的求导问题转化成了两个简单的函数求导问题,然后几步就完成了这个函数的求导。化繁为简,这就是复合函数的求导的核心意义。
1.5.6 导函数的除法运算
虽然除法和乘法也是一对反义词,但它们的求导公式是完全不同的。除法的求导可以说是最难的,所以我们单独拿出来讲。
它为什么困难呢?上面我们证明减法求导的时候,是把减法转化成加法和乘负一(更「专业」的说法是乘 相反数 ,如果你学过这个词的话),然后利用加法求导公式得到的。你肯定很容易想到:那么,除法求导的时候,我们是不是可以把除法转化成乘法和乘一个什么东西呢?
答案是:不可以。首先我们要知道,运算是有好几个不同层次的,最低级的是加减,而乘除是比它们俩高一层的。 注意注意!看「减法可以转化成加法和乘负一」这句话里的几个词:
这里的「减」和「加」是相对应的,而「乘」是比加减更高一层的计算!
而我们想象的:
这里的「除」和「乘」是相对应的,但是「乘」不是比乘除更高一层的计算!
所以,想要对应上前一节的思考方式,也应该是:
其中的「XXX」必须得是一种比乘除法还要高一层的计算才合理。
这个超高级的计算是什么呢?就是幂运算!所以,除法求导的时候,我们应当把除法转化成乘法和乘一个幂运算的结果:
或者用更简单的数学语言来说,就是:
\[\frac{f(x)}{g(x)}=f(x)\times \left[g(x)\right]^{-1}.\]
注意
\(\left[g(x)\right]^{\text{xxx}}\) 我们习惯上简写成 \(g^{\text{xxx}}(x)\),这里用方括号括起来是方便你理解的。后面我们就不再用方括号,直接写成 \(g^{\text{xxx}}(x)\) 了。
接下来让我们仿照算减法求导公式时的做法,利用一下乘法求导公式!我们知道,乘法的规则是对第一个式子求导,乘第二个;再对第二个式子求导,乘第一个。然后加起来。
「对第一个式子求导,乘第二个」是:
\[f^{\prime}(x)\times g^{-1}(x),\]
唔,这部分看起来很简单嘛!
「对第二个式子求导,乘第一个」是:
\[f(x)\times \left[g^{-1}(x)\right]',\]
新问题又来了,这里的 \(g^{-1}(x)\) 怎么求导呢?我们好像没有学过这个东西啊!
别急,再想想,既然气氛都烘托到这了,肯定是有办法的。
我们到底在哪里提过关于幂的求导呢?
我们到底在哪里提过关于幂的求导呢?
我们到底在哪里提过关于幂的求导呢?
在继续之前,请你再三思考一下,翻一翻之前的内容,看看有没有提到过,然后再往下看。
。
。
。
。
。
。
。
。
。
。
。
。
。
。
。
没错,还是在 1.5.2 节给你的简单实用的公式表里面,有关于幂的求导公式,而且当时我们还叫它「初等函数大杀器」呢:
\[(ax^n)'=nax^{n-1}.\]
这个式子是说,对于 \(ax^n\) 这个式子,它的导数是 \(nax^{n-1}\)。比如,对于 \(x^2\),它的导数是 \(2x^{2-1}\);对于 \(2x^3\),它的导数是 \(2\times 3x^{3-1}\)。
所以,看起来我们可以对于 \([g(x)]^{-1}\) 用上面的公式求导。有个小问题是:\(g(x)\) 并不是 \(x\) 啊?那我们怎么用呢?
这里要用到我们的另一个大杀器了:复合函数。我们可以令 \(f(x)=x^{-1}\),那 \([g(x)]^{-1}\) 不就是 \(f(g(x))\) 了吗?
来试试看!我们把复合函数的求导公式代入进去。首先计算 \(f(x)\) 的导数:
\[f'(x)=\left(x^{-1}\right)'=-1\times x^{-2} = -x^{-2}.\]
注意,这里的 \(x^{-2}\) 其实就是 \(\frac{1}{x^2}\),所以 \(f'(x)=-\frac{1}{x^2}\)。那么,\(f'(g(x))=-\frac{1}{g^2(x)}\)。
所以呢,我们可以继续按照复合函数的求导公式来计算:
\[ \begin{aligned} \left(\left[g(x)\right]^{-1}\right)'&=[f(g(x))]'\\ &=f'(g(x))g'(x)\\ &=-\frac{1}{g^2(x)}\times g'(x)\\ \end{aligned} \]
看起来我们终于解决了 \([g(x)]^{-1}\) 的导数,它就是 \(-\frac{1}{g^2(x)}g'(x)\)。耶✌!
乘胜追击,让我们完成这个绕了山路十八弯的除法求导公式。「对第二个式子求导,乘第一个」现在就是:
\[f(x)\times \left[g^{-1}(x)\right]'=-f(x)\frac{1}{g^2(x)}g'(x).\]
所以,最终的除法求导公式是把它和「对第一个式子求导,乘第二个」加起来,也就是下面两个加起来:
\[-f(x)\frac{1}{g^2(x)}g'(x)+f^{\prime}(x)\times g^{-1}(x)\]
经过一串草稿纸上的暴力分母通分,我们得到了最终的除法求导公式:
\[\left[\frac{f(x)}{g(x)}\right]'=\frac{f^{\prime}(x)g(x)-f(x)g^{\prime}(x)}{g^2(x)}.\]
真是「道路阻且长」啊。折腾了这么多得到的除法公式,结果还这么复杂,大概可以排进我们心目中「我最讨厌的导数公式」前三名了吧?
再小结一下,到目前为止,我们已经学会了求导的以下几种方法:
- 一些通用的求导公式
- 加减乘除的求导公式
- 复合函数的求导公式
对于水平稍高的同学,现在已经可以回头完成我们的「五年高考,三年模拟」了。快去试试吧(笑)下次更新会公布正确答案。
PS:下一次更新将在本周内,敬请期待~